Finance comportementale : quel impact des biais cognitifs dans la prise de décision ?
Il est déjà difficile d’acquérir une culture financière solide, mais il est encore plus difficile de s’en servir correctement pour prendre des décisions financières. En effet, dans ce domaine comme dans bien d’autres, nos choix et nos décisions sont inconsciemment influencés par ce qu’on appelle des « biais cognitifs » ou des « illusions cognitives » qu’il est par essence difficile de reconnaître puisqu’ils viennent de notre propre cerveau (parfois avec « l’aide » d’influences extérieures).
Système 1 et système 2
Pour décrypter ces biais, le prix Nobel d’économie Daniel Kahneman (qui était à la base un psychologue) nous explique qu’il existe une pensée intuitive (qu’il appelle « système 1 ») qui génère des solutions rapides presque « réflexe », et une pensée plus lente, qui se base sur l’examen de faits, la comparaison de solutions, la recherche d’information, etc. (qu’il appelle « système 2 »).
Le système 2 est coûteux en temps et en énergie, et de plus lent (ce qui dans certains cas où notre survie est en jeu n’est pas satisfaisant). Notre cerveau tend donc à privilégier le système 1, et à réserver le système 2 pour « contrôler » le fonctionnement intuitif si nécessaire et le corriger si nécessaire (comme lorsqu’on part de chez soi avec le trajet habituel et qu’on s’aperçoit qu’on doit se rendre à un autre endroit).
Les biais viennent de ce mélange de modes de pensées : alors qu’on croit toujours qu’une décision ou un choix est prise de manière « rationnelle », on se laisse souvent guider par des modes de pensée « automatiques » dont on n’est pas conscient.
Comme beaucoup d’illusions (par exemple l’illusion d’optique ci-dessous) en prendre conscience permet de « se méfier de soi-même » et de décider plus consciemment d’allouer du temps (de réflexion) et des ressources (se renseigner, demander des avis divers), aux sujets qui en vaillent la peine… tout en laissant son intuition et ses habitudes guider l’action pour d’autres.

Note : ces deux lignes sont de la même longueur. Mais même quand on l’a mesuré, on a du mal à le croire.
Les biais cognitifs et leurs conséquences en matière financière
Voici une liste de quelques « biais cognitifs » bien connus, ayant des conséquences possibles en matière financière.
L’excès de confiance – L’être humain (et pas seulement français) a une forte capacité à surestimer ses compétences, surtout sur des sujets qu’il ne connaît pas. Cela peut conduire à des décisions très hasardeuses (par exemple du trading en ligne d’actions, ou de crypto-monnaies).
Il faut donc savoir distinguer « l’intuition » du professionnel – qui est le résultat de l’entraînement de son cerveau par une longue expérience, et qu’il saura confronter à des analyses poussées – et « l’intuition » de l’amateur, qui est une manière pour le cerveau de se sentir confortable avec une décision prise totalement au hasard, ou sous l’influence d’une émotion, sans avoir besoin de se « fatiguer » à se mettre en mode « système 2 ». Il faut donc avant tout se méfier… de soi-même.
Le biais de confirmation – Une fois une décision prise ou une opinion ancrée, notre cerveau doit faire un effort important pour changer d’avis, et préfère garder une « cohérence » agréable, quitte à interpréter de manière biaisée les informations extérieures. On accorde donc naturellement une valeur plus importante aux faits qui confirment une opinion ou une décision, et on a tendance à minorer ceux qui vont dans le sens contraire.
Le biais de confirmation va bien sûr renforcer le biais de confiance : on a toujours tendance à rechercher les preuves que l’on a « raison » (alors que le raisonnement scientifique consiste à l’inverse à toujours chercher les éléments qui permettent de réfuter une hypothèse ou une théorie).
Le biais de disponibilité – Comme le système 1 fonctionne très vite, il va toujours chercher à utiliser le minimum de données. Ainsi, les premières informations disponibles vont nous influencer très fortement. Cela nous rend très vulnérables à la manipulation : comment les informations sont présentées, dans quel ordre, sous quelle forme.
Un exemple très connu est celui de l’ancrage des prix. Le premier prix annoncé (par exemple le prix de vente d’un bien immobilier) va constituer une référence dont il est difficile de se défaire (on va penser à « négocier moins 10% » plus facilement qu’à proposer une autre référence de prix). Il est alors crucial de se donner d’autres sources d’information (d’autres « ancres », par exemple une étude de marché) pour pouvoir contrer ce biais.
Le biais de possession (qui s’applique plus à des biens « réels » que financiers), qui fait qu’on accorde plus de prix à une chose quand on la possède, même quand elle a une valeur de marché (bien connu des collectionneurs).
Le biais de représentation qui fait que l’évocation de cas particuliers ou de descriptions (qui nous raccrochent à des « images » mentales) ont beaucoup plus d’impact que des raisonnements abstraits. C’est ce qui conduit aussi à surestimer les événements rares (« attaques de requins ») et en général à très mal évaluer les probabilités. Ce biais peut-être à l’origine de bien des manipulations, voire des arnaques : il ne faut pas se méfier que de soi-même en matière financière.
Le biais d’action qui face à un problème nous souffle qu’il faut absolument “prendre une décision” alors même que “ne rien faire” peut être la bonne décision, par exemple en cas d’agitation sur les marchés financiers (les gardiens de but plongent presque toujours d’un côté ou de l’autre face à un tireur de penalty, alors que les tireurs tirent au centre dans presque 30% des cas).
L’aversion au risque
L’aversion au risque, enfin, mérite une place particulière dans l’étude des décisions financières, puisque beaucoup d’entre elles portent sur le futur qui est incertain et donc potentiellement risqué : une décision pourrait entraîner un gain ou une perte. On sait même qu’en général une possibilité de gain significatif dans l’avenir s’accompagne en général d’un risque de perte.
Ce qu’on appelle l’aversion au risque repose donc d’abord sur une aversion à la perte (si on vous propose un ticket de loto gratuitement avec uniquement le « risque » de gagner vous allez l’accepter). Or ce biais est profondément ancré dans le comportement humain : devant un choix consistant à gagner ou perdre une somme d’argent avec la même probabilité la plupart des gens vont choisir une approche conservatrice (surtout si l’enjeu est important), sauf s’ils ont désespérément besoin du gain (et donc « rien à perdre »).
Le « biais » de l’aversion au risque est donc le « réflexe » consistant à préférer l’option non risquée dans ses décisions, sans examiner réellement les cas où la probabilité de gagner (et donc de s’enrichir) peut-être avantageuse, et la perte possible peut-être économiquement supportable (si la lecture même de la phrase « perte économiquement supportable » engendre un malaise, c’est que le biais de l’aversion au risque est présent). C’est le cas par exemple d’un placement en actions (diversifié et sur le long terme – la précision est essentielle).
Un des moyens d’éviter d’être bloqué par la « peur du risque » est de mettre en place un « contrôle du risque » : savoir précisément combien on peut se permettre de placer sur des actifs risqués, comprendre de combien est la perte maximum (et donc de pas risquer de « tout perdre »). On reconnaît là la démarche plus « coûteuse » du « système 2 ».
Paradoxalement, l’aversion à la perte peut provoquer dans certains cas une prise de risque excessive, quand c’est « l’idée de la perte » qui est insupportable plus que le montant lui-même. C’est le cas du joueur du casino qui va continuer à jouer pour « se refaire » ou de l’investisseur initial qui ne veut pas « couper ses pertes ». Cette fois-ci, ce qui empêche une évaluation rationnelle, c’est l’envie de ne pas avoir de perdre son investissement initial, plus que celle de ne pas prendre de risques.
Bibliographie
- Pour aller plus loin, lire en priorité Daniel Kahneman (« Système 1 Système 2 ») ou Richard Thaler, autre prix Nobel d’économie (« La psychologie des choix »).
- Plus aisé à lire et ouvrage de référence des marketeurs et politiciens, « Nudge ». Des auteurs comme Dan Ariety emploient un ton moins académique, voire humoristique (par exemple « Dollar et bon sens » qui regorge d’anecdotes sur les comportements d’achat).
- Parmi les français, citons « La psychologie de l’investisseur : Les biais comportementaux et leurs impacts sur la performance » par Daniel Egan ou « Petit traité de manipulation à l’usage des honnêtes gens » par Robert-Vincent Joule et Jean-Léon Beauvois.
Auteur : Nicolas Schimel
 Dans le premier cas décrit plus haut, la personne commence au point A, puis doit choisir entre d’une part arriver au point C de façon certaine et d’autre part avoir une probabilité de 50% de rester au point A et une probabilité de 50% d’arriver au point B. Dans le second cas, elle commence au point B, puis doit choisir entre d’une part arriver au point C de façon certaine et d’autre part avoir une probabilité de 50% de rester au point B et une probabilité de 50% d’arriver au point C. Dans les deux cas, en pratique, la personne doit choisir entre finir au point C de manière certaine d’une part et d’autre part finir au point A avec une probabilité de 50% ou au point B avec une probabilité de 50%.
Dans le premier cas décrit plus haut, la personne commence au point A, puis doit choisir entre d’une part arriver au point C de façon certaine et d’autre part avoir une probabilité de 50% de rester au point A et une probabilité de 50% d’arriver au point B. Dans le second cas, elle commence au point B, puis doit choisir entre d’une part arriver au point C de façon certaine et d’autre part avoir une probabilité de 50% de rester au point B et une probabilité de 50% d’arriver au point C. Dans les deux cas, en pratique, la personne doit choisir entre finir au point C de manière certaine d’une part et d’autre part finir au point A avec une probabilité de 50% ou au point B avec une probabilité de 50%. D’autre part, comme on le voit sur le graphique ci-dessus qui représente une courbe d’utilité dans la théorie des perspectives, cette courbe a une forme en S et présente une asymétrie par rapport au point de référence.
D’autre part, comme on le voit sur le graphique ci-dessus qui représente une courbe d’utilité dans la théorie des perspectives, cette courbe a une forme en S et présente une asymétrie par rapport au point de référence. On voit que, dans ce cas, tout se passe comme dans la théorie de l’utilité espérée. Le graphique représente le cas où l’on commence par donner 2 000€ à quelqu’un, puis on lui demande de choisir entre recevoir 500€ en plus de façon certaine et recevoir 1 000€ en plus avec une probabilité de 50%. Comme la courbe d’utilité est concave dans le cas des gains, c’est-à-dire que l’utilité marginale est décroissante, l’objectif de maximisation de l’utilité conduit à préférer l’option sans incertitude, conformément à ce que font la plupart des gens en pratique.
On voit que, dans ce cas, tout se passe comme dans la théorie de l’utilité espérée. Le graphique représente le cas où l’on commence par donner 2 000€ à quelqu’un, puis on lui demande de choisir entre recevoir 500€ en plus de façon certaine et recevoir 1 000€ en plus avec une probabilité de 50%. Comme la courbe d’utilité est concave dans le cas des gains, c’est-à-dire que l’utilité marginale est décroissante, l’objectif de maximisation de l’utilité conduit à préférer l’option sans incertitude, conformément à ce que font la plupart des gens en pratique.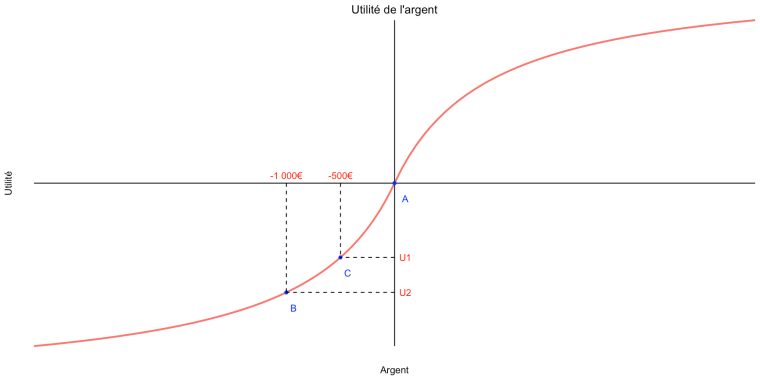 On voit que, comme la courbe d’utilité est convexe dans le cas des pertes, par rapport au point de référence, la différence entre U1 et l’utilité au point de référence est bien plus grande que celle entre U1 et U2.
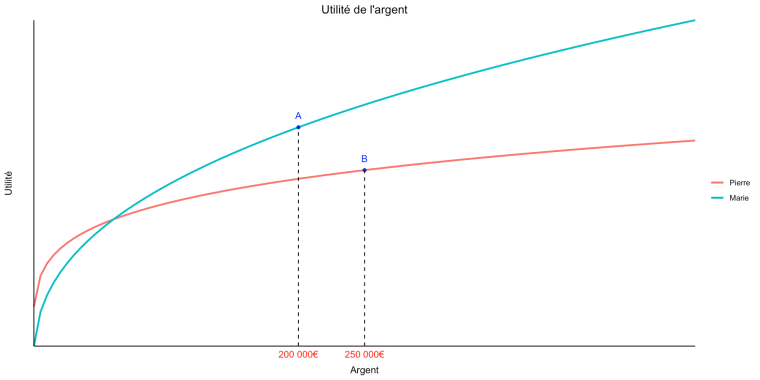
On voit que, comme la courbe d’utilité est convexe dans le cas des pertes, par rapport au point de référence, la différence entre U1 et l’utilité au point de référence est bien plus grande que celle entre U1 et U2. L’utilité marginale décroissante de l’argent se manifeste par le fait que la pente de la courbe est de moins en moins forte à mesure que Pierre a plus d’argent. Si Pierre n’a pas beaucoup d’argent, même une petite some d’argent supplémentaire peut entraîner pour lui un gain significatif d’utilité, mais s’il a déjà beaucoup d’argent alors il ne dérivera guère plus d’utilité même si on lui donne une somme d’argent importante.
L’utilité marginale décroissante de l’argent se manifeste par le fait que la pente de la courbe est de moins en moins forte à mesure que Pierre a plus d’argent. Si Pierre n’a pas beaucoup d’argent, même une petite some d’argent supplémentaire peut entraîner pour lui un gain significatif d’utilité, mais s’il a déjà beaucoup d’argent alors il ne dérivera guère plus d’utilité même si on lui donne une somme d’argent importante. On voit que, même si l’utilité marginale de l’argent est décroissante dans les deux cas, elle décroît beaucoup plus rapidement dans le cas de Pierre que dans celui de Marie. Autrement dit, pour Marie comme pour Pierre, la même somme d’argent en plus leur procurera moins d’utilité supplémentaire s’ils ont déjà beaucoup d’argent que s’ils en ont peu, mais c’est beaucoup plus vrai pour Pierre que pour Marie.
On voit que, même si l’utilité marginale de l’argent est décroissante dans les deux cas, elle décroît beaucoup plus rapidement dans le cas de Pierre que dans celui de Marie. Autrement dit, pour Marie comme pour Pierre, la même somme d’argent en plus leur procurera moins d’utilité supplémentaire s’ils ont déjà beaucoup d’argent que s’ils en ont peu, mais c’est beaucoup plus vrai pour Pierre que pour Marie.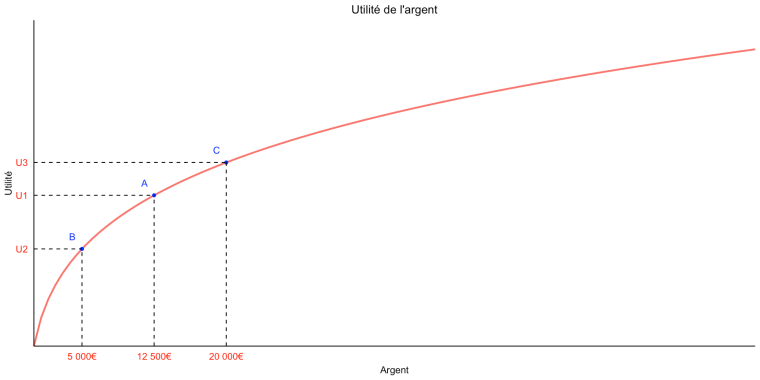 À présent supposons qu’on propose à Pierre, qui possède à ce moment-là 12 500€, le pari suivant : il a une chance sur deux de gagner 7 500€ et une chance sur deux de perdre 7 500€. Dans le premier cas, il passe du point A au point C sur la courbe, alors que dans le second cas il passe du point A au point B.
À présent supposons qu’on propose à Pierre, qui possède à ce moment-là 12 500€, le pari suivant : il a une chance sur deux de gagner 7 500€ et une chance sur deux de perdre 7 500€. Dans le premier cas, il passe du point A au point C sur la courbe, alors que dans le second cas il passe du point A au point B.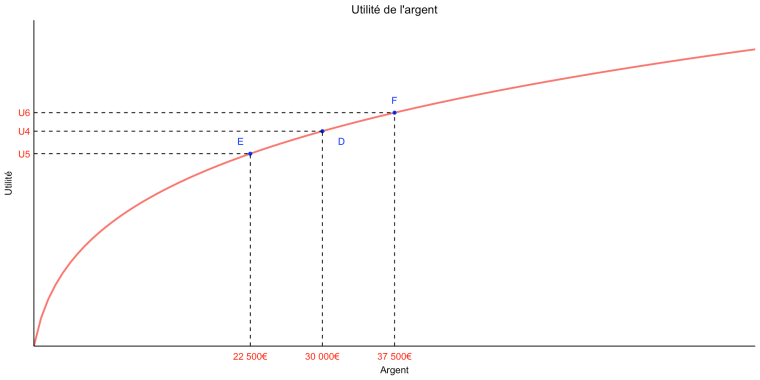 On voit que, même s’il est toujours vrai que le gain d’utilité si Pierre gagne le pari est moins important que la perte d’utilité s’il perd (la différence entre U6 et U4 est moins importante que celle entre U4 et U5), c’est beaucoup moins vrai que quand on supposait qu’il avait moins d’argent avant le pari, parce que la courbe est nettement plus aplatie au point D qu’elle ne l’était au point A dans l’exemple précédent.
On voit que, même s’il est toujours vrai que le gain d’utilité si Pierre gagne le pari est moins important que la perte d’utilité s’il perd (la différence entre U6 et U4 est moins importante que celle entre U4 et U5), c’est beaucoup moins vrai que quand on supposait qu’il avait moins d’argent avant le pari, parce que la courbe est nettement plus aplatie au point D qu’elle ne l’était au point A dans l’exemple précédent.